Graniastosłupy • MATEMATYKA NA TAK • matura, szkoła średnia, liceum, technikum, szkoła podstawowa

Graniastosłupy
- Rodzaje graniastosłupów
  - Zadanie 1.
    Pewien graniastosłup ma 45 krawędzi. Ile ma wierzchołków i krawędzi bocznych ?
  - Zadanie 2.
    Ile krawędzi ma graniastosłup, w którym liczba ścian jest o 18 mniejsza od liczby wierzchołków tego graniastosłupa?
  - Zadanie 3.
    Ile wierzchołków ma graniastosłup, w którym liczba ścian jest o 28 mniejsza od liczby krawędzi tego graniastosłupa?
  - Zadanie 4.
    Który z przedstawionych graniastosłupów prostych jest graniastosłupem prawidłowym? Odpowiedź uzasadnij ( rysunek w filmie ).
  - Zadanie 5.
    Oblicz długości krawędzi graniastosłupa prostego trójkątnego na podstawie danych z rysunku
  - Zadanie 6.
    Oblicz długość krawędzi graniastosłupa prostego, na podstawie danych z rysunku ( rysunek w filmie )
  - Zadanie 7.
    Podstawą graniastosłupa prostego jest trapez równoramienny o bokach długości : 12 cm, 5 cm, 6 cm, 5 cm. Oblicz długość wysokości tego graniastosłupa.
  - Zadanie 8.
    Cztery ściany graniastosłupa pochyłego są kwadratami o boku długości 5 cm, a odcinek EP jest jego wysokością ( rysunek w filmie ). Ściany boczne ABFE i DCGH są rombami o kącie ostrym $\alpha =30^{0}$ Oblicz długość wysokości tego graniastosłupa.
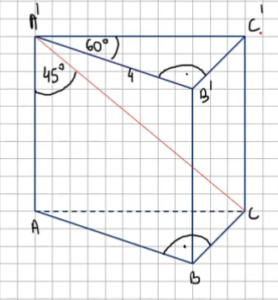
  - Zadanie 9.
    Przekątna ściany bocznej graniastosłupa prawidłowego trójkątnego ma długość cm i tworzy z krawędzią podstawy kąt $\alpha =60^{0}$ . Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
  - Zadanie 10.
    Kąt między przekątnymi sąsiednich ścian bocznych graniastosłupa prawidłowego czworokątnego jest równy 60⁰ ( rysunek w filmie ). Wykaż, że taki graniastosłup jest sześcianem.
  - Zadanie 11.
    Dłuższa przekątna podstawy graniastosłupa prawidłowego sześciokątnego ma długość 4. Dłuższa przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt 30⁰. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
  - Zadanie 12.
    Krótsza przekątna podstawy graniastosłupa prawidłowego sześciokątnego ma długość $\sqrt{3}$ , a jego wysokość jest równa 4. Oblicz długość krótszej przekątnej tego graniastosłupa oraz długość dłuższej przekątnej podstawy.
- Siatki graniastosłupów
  - Zadanie 1.
    W filmie przedstawiono siatkę graniastosłupa prostego. Oblicz pole powierzchni całkowitej tego graniastosłupa. Sporządź rysunek tego graniastosłupa.
  - Zadanie 2.
    Narysuj siatkę prostopadłościanu o wymiarach 1cm x 2 cm x 3 cm. Następnie oblicz pole tego prostopadłościanu.
  - Zadanie 3.
    Oblicz objętość graniastosłupa prostego, którego siatkę przedstawiono na rysunku w filmie.
  - Zadanie 4.
    Oblicz objętość graniastosłupa prostego, którego siatkę przedstawiono na rysunku w filmie.
- Pola i objętości graniastosłupów
  - Sześcian
    - Zadanie 1.
      Pole sześcianu jest równe 216 cm². Oblicz objętość tego sześcianu.
    - Zadanie 2.
      Objętość sześcianu jest równa 64 cm³. Oblicz pole powierzchni całkowitej tego sześcianu oraz długość przekątnej sześcianu.
    - Zadanie 3.
      Sześcian o krawędzi 4 cm przecięto płaszczyzną wyznaczoną przez równoległe przekątne podstaw. Oblicz pole otrzymanego przekroju oraz objętość sześcianu.
    - Zadanie 4.
      Sześcian o krawędzi długości 4 cm przecięto płaszczyzną przechodzącą przez przekątną BD dolnej podstawy i wierzchołek C’ górnej podstawy ( rysunek w zadaniu ). Oblicz pole trójkąta DBC’ oraz pole sześcianu.
    - Zadanie 5.
      Punkty K, L, M są środkami krawędzi BC, GH i AE sześcianu ABCDEFGH o krawędzi długości 1 ( rysunek w zadaniu ). Oblicz pole trójkąta KLM oraz objętość sześcianu.
  - Prostopadłościan
    - Zadanie 1.
      Oblicz pole powierzchni całkowitej oraz objętość prostopadłościanu o wymiarach 6 cm, 15 cm, 20 cm.
    - Zadanie 2.
      Oblicz pole powierzchni całkowitej oraz objętość prostopadłościanu o przekątnej długości 10 cm i krawędziach podstawy długości 4 cm i 5 cm.
    - Zadanie 3.
      Oblicz pole powierzchni całkowitej oraz objętość prostopadłościanu o przekątnej długości 8 cm tworzącej z płaszczyzną podstawy kąt 30⁰ wiedząc, że jedna z krawędzi podstawy ma długość 4 cm.
    - Zadanie 4.
      Oblicz objętość prostopadłościanu wiedząc, że jego przekątna tworzy z płaszczyzną podstawy kąt 60^o, a długości podstaw to 5 cm i 12 cm.
    - Zadanie 5.
      Pole powierzchni całkowitej prostopadłościanu jest równe 198. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to 1:2:3. Oblicz długość przekątnej tego prostopadłościanu.
  - Graniastosłup prawidłowy czworokątny
    - Zadanie 1.
      Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 5 cm. Oblicz pole powierzchni całkowitej tego graniastosłupa, jeśli przekątna jego ściany bocznej tworzy z krawędzią podstawy kąt 30⁰.
    - Zadanie 2.
      Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 5 cm. Oblicz pole powierzchni całkowitej tego graniastosłupa, jeśli przekątna jego ściany bocznej tworzy z krawędzią boczną kąt 30⁰.
    - Zadanie 3.
      Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 5 cm. Oblicz pole powierzchni całkowitej tego graniastosłupa, jeśli przekątna jego ściany bocznej tworzy z przekątną graniastosłupa kąt 30⁰.
    - Zadanie 4.
      Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe 16 cm². Oblicz objętość tego graniastosłupa, jeśli jego przekątna ma długość 9 cm.
    - Zadanie 5.
      Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 4 cm. Oblicz długość przekątnej tego graniastosłupa, jeśli tworzy ona z przekątną podstawy kat 30⁰. Oblicz pole powierzchni bocznej tego graniastosłupa.
    - Zadanie 6.
      Pole powierzchni bocznej graniastosłupa prawidłowego czworokątnego jest równe $48\sqrt{3}$ cm². Przekątna ściany bocznej tworzy z krawędzią boczną kąt 30⁰. Oblicz długość tej przekątnej oraz objętość tego graniastosłupa.
  - Graniastosłup prawidłowy trójkątny
    - Zadanie 1.
      Przekątna ściany bocznej graniastosłupa prawidłowego trójkątnego tworzy z krawędzią podstawy kąt $\alpha =30^{0}$ . Oblicz pole powierzchni całkowitej tego graniastosłupa, jeżeli krawędź boczna ma długość 6 cm.
    - Zadanie 2.
      Wysokość graniastosłupa prawidłowego trójkątnego jest równa 8, a jego objętość wynosi $32\sqrt{3}$ . Oblicz długość krawędzi podstawy tego graniastosłupa i pole powierzchni całkowitej.
    - Zadanie 3.
      Przekątna ściany bocznej graniastosłupa prawidłowego trójkątnego tworzy z krawędzią podstawy kąt 30⁰. Oblicz pole powierzchni bocznej tego graniastosłupa, jeżeli pole podstawy tego graniastosłupa wynosi $\frac{9\sqrt{3}}{4}$ .
    - Zadanie 4.
      Przekątna ściany bocznej graniastosłupa prawidłowego trójkątnego ma długość 10. Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa, jeżeli długość wysokości podstawy jest równa $\sqrt{3}$ .
  - Graniastosłup prawidłowy sześciokątny
    - Zadanie 1.
      Dłuższa przekątna podstawy graniastosłupa prawidłowego sześciokątnego ma długość 4. Dłuższa przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt 30⁰. Oblicz objętość tego graniastosłupa.
    - Zadanie 2.
      Krótsza przekątna podstawy graniastosłupa prawidłowego sześciokątnego ma długość $\sqrt{3}$ , a jego wysokość jest równa 4.Oblicz objętość i długość krótszej przekątnej tego graniastosłupa.
    - Zadanie 3.
      Krótsza przekątna graniastosłupa prawidłowego sześciokątnego ma długość $4\sqrt{3}$ . Wysokość graniastosłupa jest trzy razy dłuższa od krawędzi podstawy. Oblicz objętość tego graniastosłupa.
    - Zadanie 4.
      Dłuższa przekątna graniastosłupa prawidłowego sześciokątnego tworzy z płaszczyzną podstawy kąt 60⁰ . Krótsza przekątna podstawy tego graniastosłupa jest równa $2\sqrt{3}$ . Oblicz pole powierzchni całkowitej tego graniastosłupa.
  - Inne graniastosłupy
    - Zadanie 1.
      Podstawą graniastosłupa prostego jest trójkąt równoramienny o jednym z kątów 120⁰ i ramionach długości 8 cm. Oblicz pole powierzchni bocznej tego graniastosłupa, jeżeli jego wysokość jest równa 11 cm.
    - Zadanie 2.
      Podstawą graniastosłupa prostego jest romb o kącie ostrym 30⁰ i boku długości 12 cm. Oblicz pole powierzchni całkowitej tego graniastosłupa, jeśli jego wysokość jest równa 8 cm.
    - Zadanie 3.
      Podstawą graniastosłupa prostego jest trapez równoramienny o bokach długości : 12 cm, 5 cm, 6 cm, 5 cm. Oblicz długość wysokości tego graniastosłupa, jeśli pole powierzchni całkowitej tego graniastosłupa jest równe 492 cm², następnie oblicz objętość tego graniastosłupa.
    - Zadanie 4.
      Cztery ściany graniastosłupa pochyłego są kwadratami o boku długości 5 cm, a odcinek EP jest jego wysokością ( rysunek w filmie ). Ściany boczne ABFE i DCGH są rombami o kącie ostrym $\alpha =60^{0}$ Oblicz objętość tego graniastosłupa.
  - Zadania praktyczne
    - Zadanie 1.
      Krawędź podstawy pudełka w kształcie graniastosłupa prawidłowego czworokątnego ma długość 10 cm. Oblicz ile cm² papieru należy zużyć, aby okleić całe pudełko, jeśli przekątna jego ściany bocznej tworzy z krawędzią podstawy kąt 60⁰. Podaj potrzebną ilość papieru doliczając 10% na ścinki.
    - Zadanie 2.
      Skrzynka na kwiaty ma kształt graniastosłupa o podstawie trapezu równoramiennego ( odczytaj dane z rysunku w filmie ). Czy zmieści się w niej 30 dm³ ziemi?
    - Zadanie 3.
      Stodoła ma kształt przedstawiony na rysunku w filmie. Na strychu stodoły zgromadzono siano. Ile metrów sześciennych siana możemy zgromadzić na strychu, jeżeli możemy wykorzystać 90% objętości strychu?
    - Zadanie 4.
      Do akwarium w kształcie prostopadłościanu o wymiarach podstawy 30 cm x 50 cm i wysokości 40 cm, wypełnionego wodą do $\frac{3}{4}$ wysokości, wrzucono dwie kostki sześcienne o krawędzi podstawy 10 cm. O ile cm podniósł się poziom wody w akwarium?