Wszystkie filmy: Rodzaje graniastosłupów
- Zadanie 1.
Pewien graniastosłup ma 45 krawędzi. Ile ma wierzchołków i krawędzi bocznych ?
- Zadanie 2.
Ile krawędzi ma graniastosłup, w którym liczba ścian jest o 18 mniejsza od liczby wierzchołków tego graniastosłupa?
- Zadanie 3.
Ile wierzchołków ma graniastosłup, w którym liczba ścian jest o 28 mniejsza od liczby krawędzi tego graniastosłupa?
- Zadanie 4.
Który z przedstawionych graniastosłupów prostych jest graniastosłupem prawidłowym? Odpowiedź uzasadnij ( rysunek w filmie ).
- Zadanie 5.
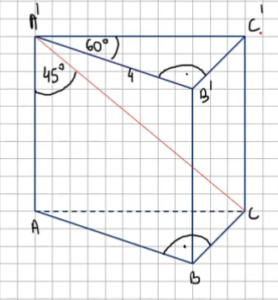
Oblicz długości krawędzi graniastosłupa prostego trójkątnego na podstawie danych z rysunku
- Zadanie 6.
Oblicz długość krawędzi graniastosłupa prostego, na podstawie danych z rysunku ( rysunek w filmie )
- Zadanie 7.
Podstawą graniastosłupa prostego jest trapez równoramienny o bokach długości : 12 cm, 5 cm, 6 cm, 5 cm. Oblicz długość wysokości tego graniastosłupa.
- Zadanie 8.
Cztery ściany graniastosłupa pochyłego są kwadratami o boku długości 5 cm, a odcinek EP jest jego wysokością ( rysunek w filmie ). Ściany boczne ABFE i DCGH są rombami o kącie ostrym
Oblicz długość wysokości tego graniastosłupa.
- Zadanie 9.
Przekątna ściany bocznej graniastosłupa prawidłowego trójkątnego ma długość cm i tworzy z krawędzią podstawy kąt
. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
- Zadanie 10.
Kąt między przekątnymi sąsiednich ścian bocznych graniastosłupa prawidłowego czworokątnego jest równy 600 ( rysunek w filmie ). Wykaż, że taki graniastosłup jest sześcianem.
- Zadanie 11.
Dłuższa przekątna podstawy graniastosłupa prawidłowego sześciokątnego ma długość 4. Dłuższa przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt 300. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
- Zadanie 12.
Krótsza przekątna podstawy graniastosłupa prawidłowego sześciokątnego ma długość
, a jego wysokość jest równa 4. Oblicz długość krótszej przekątnej tego graniastosłupa oraz długość dłuższej przekątnej podstawy.
- Zadanie 1.